Relativity's maths are circular and in error? Was this deliberate?

Why did Einstein add Riemannian geometry, and invent the space-time dimension, if not to save his equations? And why was Voigt's transformation, not based on Relativistic assumptions ignored?

We already know that general relativity must be altered. By predicting points of infinite density – singularities – classical general relativity predicts its own down-fall….When a theory predicts singularities such as infinite density and curvature, it is a sign that the theory must somehow be modified. (Stephen Hawking, A Briefer History of Time, 2005, pp. 102, 84; Black Holes and Baby Universes, 1994, p. 92)

Claim

Einstein’s Relativity yields results which are in conflict with the postulates upon which it is based namely:

1. Space time curvature is the basis of General Relativity (a demonstrably false and unproven concept),

2. Physical laws are the same in all frames of reference (equivalency). This is also false (see below) (Bertschinger, 1999).

The above are tautological as summarised below. In order to produce his equivalency through mathematical models only, namely tensor calculus equations, Einstein had to invent the curvature of space time. Logically, this means that his postulates are circular and incorrect. You see this in the maths.

There is at least one significant error in Einsteinian maths which impact the derivations. This error must have been known by Einstotle and those within the discipleship of Relativity. Intelligent undergraduates in physics have no doubt uncovered the error and raised objections, only to be beaten down by dogmatic high priests who demand bended knees and subservience to Relativity.

Bait, Switch

Relativity uses 13 tensors in its canon. It is fair to say that few truly understand them. This allows the Relativists to use bait and switch. If you critcise the canonical gospels of Relativity you don’t understand them. If you find mathematical or observational flaws in Relativity you have used the ‘wrong’ Relativity. Depending on the case example, you should have used ‘Lorentzian Transformations’, not Einsteinian Transformations and within this corpus there is the ‘Special Theory of Relativity’ transformations which should not be confused with the ‘General Theory of Relativity’ transforms. As with anything in ‘The Science’, the theory is of course, never wrong.

Tensor construction….does it really mean anything? Speed of light is variant, not invariant, a fact that even Einstotle admitted.

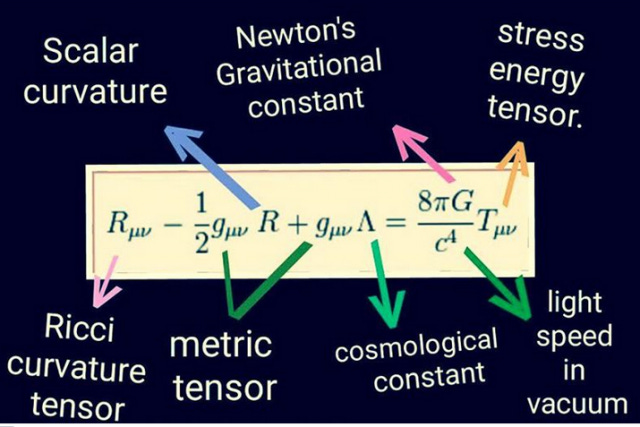
Tensors

Einstotle’s wizardry was premised on ‘tensor calculus’ (Einstein, 1914). This was developed by Ricci in 1901 and is often called Ricci calculus. If properly applied, tensor calculus can be a useful tool. Tensor calculus is an extension of differential calculus and employs a ‘vector’ within algebraic equations.

· Vector = a linear map that produces a scalar, with the map containing both magnitude and direction. Examples of vector quantities include velocity, acceleration, momentum, displacement, and forces, such as weight and friction.

· Scalar = a quantity that only has a magnitude or size. Examples of scalar quantities include pure numbers, mass, speed, temperature, energy, volume, and time.

· Matrix = a representation of a map that includes 2 vectors.

A vector is used to transfer one ‘form’ into another form. For example, in linear algebra one can take vector ν and the matrix A, to derive a new vector by multiplying the matrix by the vector v, or ν * A = ω where this symbol is new vector. A tensor is in essence a matrix.

From a physical entity point of view, the objective is to combine ‘linear’ concepts such as a mass, with motion, friction, or measurement of the mass over time, or its ‘dilation’. A tensor can therefore be interpreted as something that brings together different components of the same entity, without adding them together in a scalar or a simple vector sense of addition. An example would be just simply adding 2 elements and their masses and see how that might affect velocity or friction.

Woldemar Voigt (1887) derived a transformation, which is very similar to the Lorentz transformation. Einstein’s entire model is based on Lorentz Transformations. Voigt used an elastic aether model which is anathema to Relativists. There is no aether in Relativity, space is a ‘vacuum’ (another false and unscientific assumption).

Voigt’s transformation disproved Relativity, or the need for Relativistic maths to explain motion, velocity and objects in dynamic or accelerated frames of reference. The cult however, will say the opposite, and claim that Voigt violated Relativity, so Voigt must be wrong, as if a maths theorem is gospel!

Relativity

Tensor calculus, is an extension of vector calculus, and is the central mechanism used to ‘prove’ Einstein’s theory of relativity. This theoretical framework attempts to understand complex relationships in spacetime or in ‘Science’ parlance, ‘the fabric of the universe’. Spacetime is a false, unproven assumption, so the entire endeavour is tautological.

You can’t ‘prove’ the existence of a 4th dimension using calculus. You have to prove the existence of the 4th dimension using mechanical, physical proofs, and then describe how it operates using calculus. This is the heart of the fraud and it is reflected in the underlying errors in its calculus.

Furthermore, tensors are based on calculus and its laws. They should obey certain transformation laws. A change of basis for a matrix or transformation should not alter the underlying map upon which the new matrix is built. This means that even though a new vector can be expressed mathematically, it is geometrically considered the same as it was before. Einstein’s maths contravene basic laws of calculus.

The problem is really this. Tensor calculus cannot, and does not, support the derivation of a relativistic theory. That is not why or how they should be used. Tensor calculus has nothing to do with ‘Relativity’. This is because tensor calculus in its pure form, is a process in which partial derivatives or the variables of interest, are arranged in a set of simultaneous equations, akin to what we use in algebra.

There can be no tautologies and no hidden forms. A hidden form means for example a single number that is used in the equation as a coefficient, but comes from somewhere else. Yet this is what occurs within Relativity’s tensor calculus.

Circular logic

If we take a simple excel spreadsheet we can see what this means. Populate your flat file with numbers and calculations. Within tensor calculus I might want to represent this as a dimensional cube called R1. For the R1 dimension, the cells might look like this:

• 00-cells: {(0,0)},{(0,1)},...;{(0,0)},{(0,1)},...;

• 11-cells: [0,1]×{0}[0,1]×{0}, {0}×[0,1],...;{0}×[0,1],...;

• 22-cells: [0,1]×[0,1],....[0,1]×[0,1],....

If you want to transform the flat file into a 3 dimensional object to capture all of the cell information and and how the numbers are transformed, you would end up with differential calculus forms, or a single number (form) in the shape of a dimensional cube or cubical grid. This will generate an infinite cubical complex acquired by dividing the Euclidean space into small, simple pieces. You are basically ‘transforming’ something that is ‘flat’ into an image which can be colour coded (why you want to do this, is a completely different story). There are no hidden numbers here.

Example

As shown below, there is a circular logic in how Einstein’s Relativity processes the equations. Take the simple image below. In a flat file or grid we have an x and y axis. If I want to find out the function within this file, or on this surface, I need to derive x and y. This is the basis of tensor calculus and its rendering.

· ∂ = indicates that the term is a partial derivative (explained in image above)

· A₁₁ to A₃₃ are the constants determined by the problem being resolved

· X, Y, Z are the variables whose values we need to calculate

· W1 etc are the sums from the equations

· * = multiply

To create the tensor, or matrix, it is necessary to integrate the equations

Take 3 simple equations which are to be transformed into a new matrix.

A₁₁*∂X+A₁₂*∂Y+A₁₃*∂Z = W₁

A₂₁*∂X+A₂₂*∂Y+A₂₃*∂Z = W₂

A₃₁*∂X+A₂₂*∂Y+A₃₃*∂Z = W₃

In the above example, imagine that the constants are scalars, X, Y, Z are eucliden variables related to vectors and W is simply the outputs. In this complexity we will need to integrate these 3 vectors, similar to the diagram below, in order to derive a new matrix (Retic, pp. 109-11).

Integration issues

The integration makes the problem obvious. To create the equations, we need to know the coefficients of A₁₁ etc, and to know that these coefficients of the partial derivatives are independent of the variables. The basic rule of calculus, including tensor calculus, is that the variables to be integrated must be completely defined in the expression itself and not hidden in other terms. We saw this in the excel example above, where there were no hidden forms.

It is because the solution of a problem in tensor calculus requires mathematical integration that it cannot be used to derive a relativistic theory. The partial derivatives in the tensor calculus matrix used to derive the General Theory of Relativity involve length. Units of measurement of length change between reference frames which differ in velocity (Blinn, 2017).

• This means that the effect of a change in elevation for a meaningful valid integration must be known. However, the effect of a change in elevation on the units of measurement for length cannot be known until the integration has been performed correctly and a valid integration cannot be performed until the effects of a change in elevation on the units of measurement for length are known. This is tautological (Lay, 2006).

• This entails that a valid derivation of gravitational theory is impossible. When used, it arbitrarily forces the gravity transformation for length to equal unity regardless of the correct value. This is an obvious and erroneous loop of circular logic.

• This is true because Einsteinian tensor calculus outputs are unsupported by Euclidean geometry. To resolve this Einstein added Riemannian geometry and curved space.

Here then we have then the crux of the problem. In fact tensor calculus is not even needed to derive vectors or matrices and it cannot support the Relativistic assumptions of Einstein. We see this reflected in the perihelion of Mercury and how Eintein described gravity which we will describe in the next post.

Bottom Line

It is well known that Relativity’s tensor calculus is inherently circular and invalid. It is also well known that space-time was injected into the General Theory of Relativity to save the equations, through the imposition of curved space time. The space-time curvature does not exist, has never been proven to exist and only exists in maths and models.

Why the hoax, if that is indeed what it is? Perhaps, pace Herbert Dingle, few really understand anything about ‘Relativity’ which gives the cult the liberty to say that critics don’t understand Relativity, or, they are using the ‘wrong Relativity’. The wizards blinding the faithful with their models and maths, and naming it ‘The Science’.

All hail.

nb; in a future post, will go through why Einstotle’s postulates are wrong and disproven (using Relativity’s own construction)

A brief history of ‘Relativity’, why, who, how and Einstein’s open plagiarism.

Einstein’s Relativity ‘Postulates’ are wrong, a short summary as to why.

Sources

Bertschinger, E., Tensor Calculus for General Relativity, 1999. https://web.mit.edu/edbert/GR/gr1.pdf

Blinn, C. Schwarzschild Solution to Einstein’s General Relativity, 2017 (for a discussion of Hilbert, Schwarzschild transformations not reproduced in this post) https://sites.math.washington.edu/~morrow/336_19/papers17/carson.pdf

Tadesse, H. A Theoretical Framework of Absolute/Relative Motion and the Speed of Light, 2018.

Lay, David C. (2006). Linear Algebra and Its Applications (3rd ed.)

A. Einstein, M. Grossmann, "Entwurf einer verallgemeinerten Relativitätstheorie und einer Theorie der Gravitation" Z. Math. Physik 62 (1914) pp. 225–261

H. Retic, ‘The Einstein Hoax: The disastrous intellectual war on common sense’, 2001.