Satellites do not prove a moving Earth and they disprove Relativity. Back to the Sagnac Effect.

NASA and other agencies use a fixed Earth in their software and systems when launching probes and satellites. They also use the Sagnac calcuations in their software and communications.

“As the discussion of the Sagnac effect indicates the fundamental question regarding the speed of light is the following: Is the speed of light constant with respect to the observer (receiver) or is it constant with respect to the chosen inertial ECI (Earth Centred Inertial) frame? Clearly the GPS range equation indicates the speed of light is constant with respect to the chosen frame….

The JPL (Jet Propulsion Laboratory) equations, used to track signals from interplanetary space probes, verify that the speed of light is with respect to the chosen frame. In the JPL equations, the chosen frame is the solar system barycentric frame….Clearly, the JPL equations treat the speed of light as constant with respect to the frame – not as constant with respect to the receivers.” (Ruyong Wang and Ronald R. Hatch, Conducting a Crucial Experiment of the Constancy of the Speed of Light Using GPS, ION GPS 58th Annual Meeting / CIGTF 21st Guidance Test Symposium, 2002, p. 500.)

The speed of light is variant. Light speed for the receiver (Earth) is not constant. There is also the vector radiation of light and energy which does not conform to the simple model of Relativity. NASA and space agencies used a fixed Earth (ECI or Earth Centred Inertial) in their software and calculations for satellites, probes and instrumentation. They don’t use ‘heliocentricity’.

The Science

As with so much of ‘the science’, ChatGPT or OpenAI replies related to scientific questions do not necessarily provide truth or reality. Questions about Global Positioing Systems (GPS) or geo-synchronous satellites are an example. Neither proves the Earth’s alleged Copernican motion, nor Einsteinian Relativity. Quite the opposite. They highlight the issues with Newtonian and Einsteinian physics.

A geosynchronous satellite is usually defined as:

“…an orbital period the same as the Earth’s rotation period. Such a satellite returns to the same position in the sky after each sidereal day, and over the course of a day traces out a path in the sky that is typically some form of analemma. A special case of geosynchronous satellite is the geostationary satellite, which has a geostationary orbit – a circular geosynchronous orbit directly above the Earth's equator. Another type of geosynchronous orbit used by satellites is the Tundra elliptical orbit.”

Does an object orbiting a complete cycle within a sidereal day (star time, 23 hours 56 minutes, 4 seconds), really prove heliocentricity?

Newtonian High Wire Act

At about 22,242 miles from our planet’s surface there is a balance of forces between gravity, the inertial forces of the Earth, the Sun, the Moon, and the stars. At this altitude the satellite will be in a geostationary orbit, remaining indefinitely in the same position in space. In the heliocentric view, the satellite needs enough speed to keep up with Earth’s rotation.

Copernican view

In the Copernican vision, given that the Earth rotates on its axis at 1054 mph at its equator, the geosynchronous satellite must be given a velocity of about 7000 mph in the west-to-east direction to keep up with Earthly rotation. Since space has reduced friction, the 7000-mph speed will be maintained mainly by the satellite’s inertia (namely its initial speed), with additional thrusts interspersed as needed to account for anomalies. If the satellite keeps the 7000 mph, it will remain at 22,242 miles above the planet and not be pulled down by the Earth’s gravity.

This follows the Newtonian model in which the inertia of the geosynchronous satellite causes it to move in a straight line, or its inertial path, but the Earth’s gravity seeks to pull it toward Earth. The satellite’s altitude above the Earth will determine the velocity needed to keep the satellite at this chosen altitude. Due to the pull of gravity, the closer the satellite is to Earth the faster it must move to counteract gravity and maintain its altitude.

The heliocentric system explains this phenomenon by viewing the Earth as rotating within a 24-hour period, while the geostationary satellite remains motionless in space. Newton’s law of gravitation provides a mathematical framework to explain the locus of the balance. In the Copernican model therefore, at a specific location on Earth right over the equator, one will see the satellite directly overhead at one specific time during the day.

All of this is sensible but….

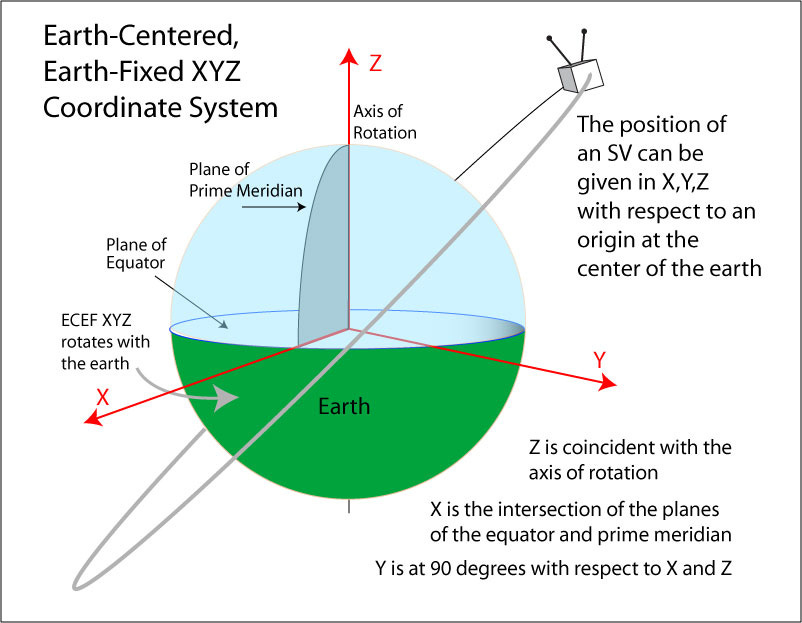
But the fact remains that NASA and other agencies usually apply a geocentric model when they launch satellites or probes near to the Earth. This is known in the industry as a ‘fixed-Earth coordinate system’. This is because it is much easier to calculate and chart the movements of satellites circling the Earth if the Earth is understood as stationary in space. Inertial forces are missing from Newtonian mechanics.

The Earth Centred Inertial or ECI model assumes a fixed, immobile, but rotating Earth. However, inertial forces also explain the rotational phenomena and the same mathematics can be applied to derive the same calculations to keep the satellite in place. GPS’ in other words do not prove anything related to heliocentricity. The important point is that they assume a fixed Earth.

Sagnac Effect

To keep the GPS within at least a meter of determining a designated location on Earth, the GPS clock must be accurate to within 4 nanoseconds, which requires a time stability ratio on the order of 1:10¹³. Atomic clocks are employed for this purpose (e.g., cesium clocks). A GPS requires frequent uploads of ‘clock corrections’ to keep everything in synch. Even when making adjustments for the Doppler effect and gravitational redshift, there still remains a margin of error. If these factors are not taken into account, a GPS could be off by as much as 11 km (6.8 miles) in one day.

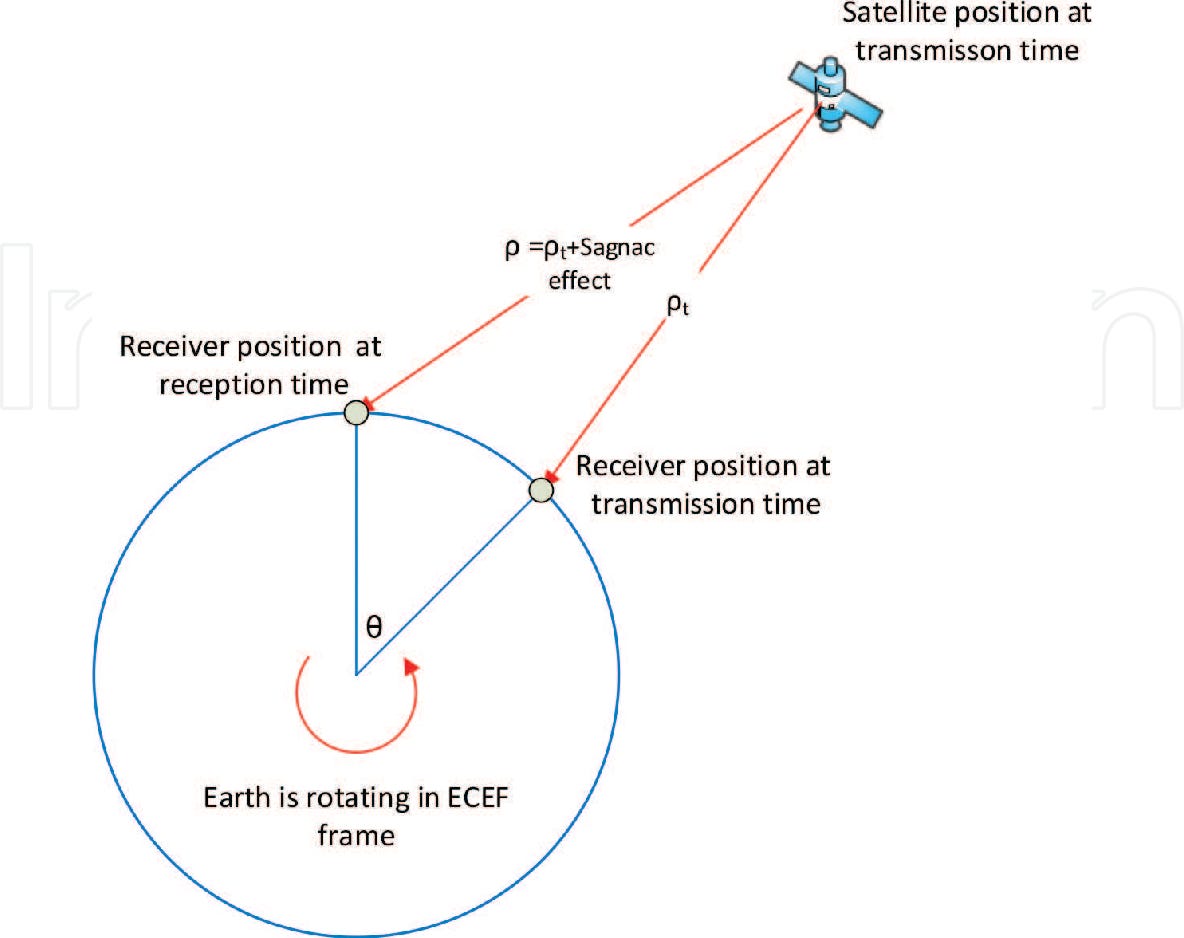
Given that a GPS system is revolving around the Earth, the signals sent from the ground arrive either at an approaching or a receding GPS satellite. The microwave beams sent to an approaching GPS satellite take 50 nanoseconds less time to reach the satellite than beams sent to a receding satellite. This is the Sagnac effect.

“The Sagnac effect is particularly important when GPS signals are used to compare times of primary reference cesium clocks at national standards laboratories far from each other….A Sagnac correction is needed to account for the diurnal motion of each receiver during signal propagation. In fact, one can use the GPS to observe the Sagnac effect” (Neil Ashby, “Relativity and the Global Positioning System,” Physics Today, May 2002)

The 50-nanosecond difference is built into the computer programs of the GPS since each satellite must, without exception, take into account the Sagnac effect (i.e., that electromagnetic waves in a moving device do not travel the same distance in the same time if they are sent out in opposite directions). This allows the GPS to keep accurate time and determine proper coordinates on Earth. The Sagnac effect proved that electromagnetic beams traveling in opposite directions will not travel at the same speed. We can therefore state:

1. The speed of light is not c but c + v or c – v, where v = velocity of the receiver, which explains why there is a 50 nanosecond difference from electromagnetic beams sent from GPS ground stations to receding or advancing GPS satellites, respectively. In the end, the GPS does not support Special Relativity.

2. The reason that the speed of light in the Earth’s atmosphere is either c + v or c – v is due to the aether which rotates around the Earth, east to west, with the rest of the universe on a 23 hour, 56 minute and 4 second sidereal rate.

3. Hence, GPS electromagnetic signals sent east-to-west travel at c + v; while those sent west-to- east travel at c – v. This difference in the speed of light is known as the Sagnac effect.

What say the Relativists? What they always say. Obfuscate and confuse.

Relativists will replace the Sagnac effect with the Lorentz transformation which they then equate into Relativity! In fact, Lorentz’s transformations assume an aether, anathema to Relativity and they have nothing to do with the physical observations of the Sagnac effect. Lorentz transformations focus on ‘mass dilation’ to explain away the failure of the 1887 Michelson-Morley experiment, which found no movement of the Earth.

In other words, as usual, ‘the science’ simply ignores the reality of the Sagnac effect which is used in GPS systems and invokes magic words and equations.

Inertial forces

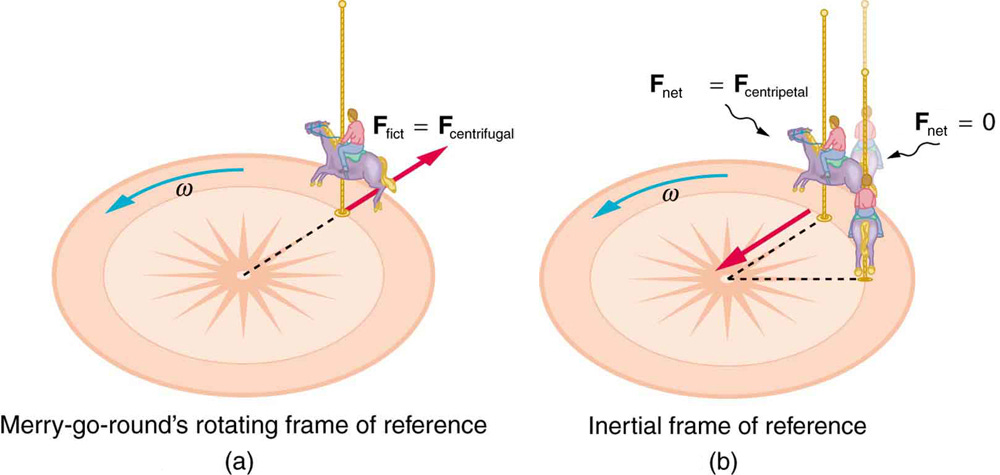
Newtonian mechanics has a defect since it cannot deal with accelerated frames of reference. It can only deal with non-accelerated or inertial frames, such as absolute space. If space is not ‘absolute’, which is what Relativity preaches, then we have a problem. Relativity means that there are accelerated frames of reference or relative motion, which cannot be resolved by Newton’s laws.

The only way Newtonian mechanics can deal with accelerated frames is to add the very things that accelerated frames produce, namely, the three inertial forces: centrifugal, Coriolis and Euler. Newtonian, Einsteinian and modern physics cannot account for, and do not explain these forces, yet they exist and must exist within the Relativity framework, even though they remain unexplained.

As noted in other posts, Mach and Einstein compensated for this Newtonian defect by incorporating accelerated frames into their physics.

Such inertial forces must be added in, when we look at the balancing force of gravity. This insertion of inertial forces is consistently done in Newtonian mechanics when predictions of movement need to be made in accelerated frames. Without adding in the three inertial forces, Newtonian mechanics would not work in accelerated frames (see other posts here on Coriolis for example).

In the case of the geosynchronous satellite, Newtonian mechanics must add the centrifugal, Coriolis and Euler forces so that the satellite can remain stationary in a rotating (accelerating) universe. This simply means that using Mach and Einstein’s postulates we cannot use geosynchronous satellites as a form of proof for heliocentricity.

Nota Bene: An alternative view

If space agencies are using a fixed Earth in launching satellites and probes, and incorporating the Sagnac effect to distance and time calculations, what is the implication?

Whether or not modernity is open to Tychonic models is a philosophical question. The Tychonic does consider accelerated frames of reference. A spinning carousal or a spinning universe are by default, accelerated frames and thus not strictly applicable in Newtonian mechanics. They are poorly explained by Relativity.

In the geo-helio-centric system for example, the Earth is not rotating; rather, the whole of space is rotating around the Earth, which carries the satellite with it. In this case we might call it a stellar-stationary satellite instead of a geostationary satellite. In this model, the Earth and the satellite are stationary while the universe, at the altitude of 22,242 miles, is rotating at 7000 mph east-to-west. Identical to the heliocentric version, the satellite must be given a velocity of 7000 mph (west-to-east) to move against the 7000-mph velocity of the rotating space (east-to-west).

The combination of the universe’s centripetal force (centrifugal plus Coriolis) against the satellite’s speed of 7000 mph, along with the Earth’s gravity on the satellite, will keep the satellite hovering above one spot on the fixed Earth. In post-Newtonian physics, a rotating universe produces the necessary centrifugal, Coriolis and Euler forces to balance out the gravitational pull from the Earth, and thus the satellite can remain fixed over one spot on the Earth at an altitude of 22,242 miles. Pace modern science and its postulates this is entirely valid. Theoretically and mathematically there is no argument against such a model.

Bottom Line

GPS’ and satellites do not prove heliocentricity. In fact, they raise more questions than answers. Further, the Sagnac effect, which disproves the invariance of light speed and Relativity, is the only way to keep GPS’ and satellites in operation.

‘The Science’ cannot explain this except to lie and claim that the Sagnac effect proves Relativity! In reality the Sagnac effect disproves the invariance of light speed and Relativity’s postulates. Nor do GPS’ or satellites indicate that the Earth is rotating, as given by satellite images to be described in the next post.

Whether the Tychonic model is correct or not, I don’t know. Universal inertia forces do exist and are poorly explained by modern physics. What is true is that the Tychonic system explains the phenomena, including the inertial, at least as well as the Copernican. Other models also exist which can ‘save the phenomena’ (gravitational relativity for example which would completely upend modern cosmology and long ages).

As outlined in this post and in many others, the proof for the Earth’s mobility and rotation is very thin indeed. It might move and spin like a lithe figure skater, but it devilishly hard to prove.

Unfortunately most people do not understand that philosophy and not observable evidence, informs most of cosmology and physics. You don’t need to believe the standard model or its philosophical narrative. You can utilise your own common sense and sensory experience and construct your own conclusions.

All hail.

Sources

Roberto de Andrade (2005) Mechanics and Electromagnetism in the Late Nineteenth Century: The Dynamics of Maxwell's Ether.

Oliver Darrigol, (2000), Electrodynamics from Ampére to Einstein

Bruce Hunt (1986), Experimenting on the Ether: Oliver J. Lodge and the Great Whirling Machine Historical Studies in the Physical and Biological Sciences, Vol. 16, No. 1 (1986), pp. 111-134 (24 pages)

M. Janssen, J. Stachel, (2004) The Optics and Electrodynamics of Moving Bodies, Max Planck. Inst. Hist. Sci.

G B Malykin, Usp Fiz Naut 170 (1325-1349) (2000); Phys Usp 43 (1229-1252) (2000)

J. E. Persson, (2010) The empirical background behind relativity, Physics Essays Vol. 23, (634-640).

C. C. Su, (2001), J. C. Eur. Phys 21, 701-715

Florentin Smarandache (2013) Unsolved problems in special and general relativity