Gödel’s 'Incompleteness Theory' and why it undermines Relativity and mathematically-based 'science'.
Maths is not science. Equations are out of context, framework-less models, which often cannot be verified and are often syntactically and semantically unproven.
Context is King
One of the issues with complex mathematics which informs Relativity and its tensor calculus ‘proofs’, is the lack of a framework and reference. The reader or the student won’t understand what the mathematical equations are performing, without the right context. This is one reason amongst many, why Relativity is not ‘truth’, not ‘validated’ and is indeed falsified.
An example:
· Observer 1: ‘He is killing them all’.
· Observer 2: ‘Who is ‘he, and what or who, is ‘them’?
· Observer 1: ‘The man is killing all of the weeds in his garden with a herbicide’.
· Observer 2: ‘Ah, so it is just a weedicide then, I was worried it was important’.
The framework and context make all the difference. Consider Einstotle’s declaration that a train crash can be ‘relatively’ interpreted by different observers.
· Observer 1 on a train: ‘We have crashed and stopped’.
· Observer 2 on a train platform: ‘What has crashed and stopped?’
· Observer 1 on the train: ‘The mountain and earth moved into our train, smashing into the engine, forcing the railcars off the track.’
· Observer 2 on the train platform: ‘No, I was watching your train. Unfortunately it crashed into the mountain and the railcars were forced off the tracks due to this impact’.
This was Einstein’s thought experiment on Relativity. Depending on your context, and observer position, the event can be framed in different ways. This means that ‘relatively’ speaking there is no truth or reality, I can use abstract mathematics to ‘prove’ both scenarios. Which ‘scenario’ I support will depend on my philosophy and observer position. This incoherence and subjectivism is what passes for ‘The Science’.
Gödel and Einstotle
In 1931 a 25-year-old Austrian mathematician, Kurt Gödel, developed the ‘Incompleteness Theorem’ as he analysed mathematical formulae and their relevancy. The theory is still valid today and has never been refuted, based as it is on simple common sense and demonstrable logic which parametrises the limits of provability in formal axiomatic and mathematical theories.
Principle 1: in a consistent and formal system named F, within which mathematical operations are carried out, there are statements of the language within F, which can be neither proven nor disproven (unless one uses an outside framework reference, or context, see the simple examples given above) and,
Principle 2: in this formal system named F, we cannot prove that the system itself is consistent, we must assume that it is internally consistent. The internal consistency of the system has a great impact on the mathematical operations but cannot be verified without the use of an external frame of reference.
The logic is pretty dense, but we can try to understand the idea using a simplified semantical form. We can view a sentence which espouses theoretical logic and forget about mathematical equations. Looking at a sentence, which is expressing a theory, Gödel’s logic can be summarised as:
T = a theory and S= a sentence, the symbols refer to semantics and syntax
What Gödel is looking for is both syntactic and semantic consistency.
Semantic consequence Γ ⊨ φ:
sentence φ is true in all models of Γ
Syntactic ‘consequence’ or Γ ⊢ φ:
sentence φ is provable from the set of assumptions Γ
From the equation above:
1. S is a syntactic consequence within T, expressed in the above as (T|-s),
2. S is provable from T in a deductive system F,
3. If this is true, it can be said that S is a semantic consequence of T (T|=s),
4. This holds in every model of T,
5. The ‘completeness theorem’ then claims that for any ‘first order’ theory T, within a ‘well orderable’ language and any sentence S in the language of T, then the equation above will be true,
6. We can therefore propose that the syntactic and semantic consequence are equivalent for first-order logic,
7. If the above does not hold true, than the theory is ‘incomplete’.
The above logic can be applied to mathematical operations inside a defined system F.
Representation
In his dense logic Gödel outlined different relationship states within a system, and its mathematics. His principles outline the ‘representability of sets’ (namely sets of numbers), and their relations in a formal system he called F. For example, the relationship below is ‘strongly representative’ within the system called F.
N = natural number, S = a set of natural numbers, there is one free variable x for every natural number n, represented in the formal system F.
A weak representation can also be formed in much the same way if there is a formula A(x), where A*x represents the formula of the language within F, such that for every natural number n:
This leads to 2 principles regarding representability:
A set of numbers (or a relation) is strongly representable if and only if it is recursive;
A set of numbers (or relation) is weakly representable if and only if it is recursively enumerable.
You can apply this to mathematical notations and formulae.
The logical elaboration is very detailed but in essence there are sets of numbers which are only weakly but not strongly representable (the key example being the set of statements provable in the system). This leads back to the 2 basic principles given at the beginning.
What does it mean?
Gödel’s theorem is very important when reviewing the philosophy of mathematics and logic. No longer can mathematics be accepted at ‘face value’. For a mathematical treatise to be ‘valid’ there must be an external framework which can be used to contextualise and confirm both the system and its associated mathematical operations, including syntactic and semantic consequences.
We see this in IT systems. I can produce programmatic code that ‘gets the job done’ and produces a valid result. Applause all around. However, my code is not and can never be, ‘a law’. It might be syntactic garbage, and semantically obtuse and you will see this when you run a code checking tool against it.
Another engineer might look at my code and become dizzy from the over-engineered and poorly constructed arcana. Yet the thing works. It is not however an ‘immanent postulate’. There are many other ‘models’ that could be written which generate the same, or a superior result and explanation. So it goes with maths - which is the basis after all of programming. Why do I need to accept tensor calculus as the only ‘code’ which ‘saves the phenomena’? Who has code checked ‘the science’ and its maths?
The conclusion is simply that in mathematics, as with computer programming, a system cannot be syntactically and semantically confirmed to be consistent and relevant unless there is a verified context including expected output.
In essence, Gödel’s theorem dismantles the long-held expectations of ‘The Science’, represented by figures such as Einstein, David Hilbert, Gottlob Frege and Bertrand Russell, who believed with a religious fervour, that a formal system inclusive of all mathematical truth could be found. Gödel’s insight negates Russell’s work on inclusive mathematical proofs as outlined in type theory and Principia Mathematica. It destroys Relativity. It also throws a dagger into the illogical hearts of ‘logical positivists’ who believe that no absolute truth can exist.
Bottom Line
Gödel’s framework is a theorem of mathematical logic, which he validated by a rigorous argument, and incontrovertible proof. His theory does not, however, ‘relativise’ mathematical truth, such as 2 + 2 = 4. It argues against the abstract usage of mathematics in domains that do not have a proper contextual reference.
Russell and Einstein both believed that mathematics and theory could replace formal physical experimentation. This was what Einstein was after, namely the elevation of Galilean thought experiments, ‘confirmed’ by abstract mathematics employed to explain the physical world, regardless of mechanical experimentation. Einstotle called himself first and foremost a philosopher.
Gödel’s theorem clearly states that a consistent formal system which is detailed and rich enough to accommodate ordinary arithmetic, is logically, syntactically and semantically, incomplete. There is simply no formal structure which can frame an all-encompassing mathematical truth. Therefore, the dreams of Einstein and Russell, to create an overarching mathematical philosophy describing all physical science is a chimera. This is one reason amongst many why a ‘unified model of everything’, trumpeted by the materialists with their ‘science’ will never happen.
The theorem also disproves the ‘immutable truth’ of Relativity. The inherent illogic of Relativity should be obvious, given that no context and no framework can be applied to its tensor calculus.
All hail.
Readings
Raatikainen, P., 2005, “On the Philosophical Relevance of Gödel’s Incompleteness Theorems,” Revue Internationale de Philosophie, 59: 513–534 [available online].
Franzén, T., 2005, Gödel’s Theorem: An Incomplete Guide to its Use and Abuse, Wellesley: A.K. Peters.





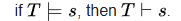





Great stuff!