Relativity and its tautological maths. The gravitational pull of the Sun on Jupiter as an example.
Many simpler and more logical explanations exist, based on Newtonian and Keplerian maths to explain how planets interact. Relativity provides an endless sequence of absurd confusions.
Dr. Arvid Reuterdahl, “The Fitzgerald-Lorentz contraction Hypothesis (the basis of Einstein’s own equations) is pure mathematical fiction which is not supported by any known and observable fact, it was invented to account for the alleged negative result in the Michelson-Morley experiment.” (‘100 Authors against Einstein’, 1930, p. 41)
Relativity was concocted to defend Copernicanism and the theory that the Earth is moving, gyrating, disco-dancing 585 million miles around the Sun, each year. It might be. But the mechancial proof for the Barber of Seville routine in space is very, very thin to non-existent.
Einstein, the great philosophical comedian and artificer, along with many others from the cult of mathematics, concocted the endless abstract inanity of Relativity to deny Michelson-Morley’s 1887 proof from light interference experiments, that no movement of this planet can be found, but an aether wind detected.
Scientology
STR is false given it does not include gravity, nor an aether. Gravity exists. So does the aether. STR was created to avoid the implications of light experiments which found an aether but no movement of this planet. GTR tried to amend STR by adding in both gravity and a ‘not ponderable’ aether. GTR therefore nullifies STR. GTR is based on circular maths and tautological ‘reasoning’ and explains nothing because it means nothing. The tensor calculus field equations are invalid. When used in reality they derive nothing.
Jupiter-Sun example
We can take a simple example, the ‘gravitational attraction between Jupiter and the Sun’. Let’s start with a comparison of mass.
Figure 1: Comparison of Jupiter with the Sun
The Sun is 1000 times bigger in mass than Jupiter, though its diameter is only about 10 times greater. Within our Solar System the Sun contains about 99.85% of the total mass. We can see that even with a planet as large as Jupiter, the gravitational attraction of the Sun must be immense. Compare Jupiter to the Earth.
Figure 2: Jupiter and the Earth
The diameter of Jupiter is roughly 11 times that of Earth, but its density of mass is 318 times greater. This gives us some idea of just how ‘massive’ Jupiter (Jove) truly is. Note there are issues and assumptions with measuring ‘mass’.1
From the above tables, if we want to derive the mass of the Sun for example, the standard equation is:
· Mass = Gravity constant x (4π^2 x a^3)/(P^2)
· ‘a’ is the semi-major axis of the orbit, and ‘P’ is the orbital period.
Assumptions
Even here, with the above standard equation, there are many assumptions which might be wrong. Why is this important? These assumptions on ‘mass’, derived from Newton, directly impact our GTR equations. We can list some obvious issues here.
1. This equation assumes there are only 2 planets. This is not how our Solar System is built.
2. The equation assumes a perfect ellipse or circle. Neither exist in reality.
3. The equation ignores the reality that planets have finite sizes and mass distributions, which affects their gravitational fields.
4. The Gravitational Constant (G) is unproven. Gravity is a weak force, roughly calculated to be 6.674 × 10⁻¹¹ m³ kg⁻¹ s⁻². This may or may not be accurate.
5. P and ‘a’ assumptions. As with gravity, the accuracy of the calculated mass depends heavily on these constants which may be wrong, especially ‘a’.
The narrative is that the equation is ‘close enough’ but anytime you see ‘constants’ or plugins there needs to be a caveat raised that the equation might well be inaccurate.
So the problem statement, a simple one, would be to use GTR and then Newtonian physics to explain the gravitational attraction between the 2 largest objects in our Solar System – Jupiter and the Sun (Jupiter’s mass is roughly 3 times that of Saturn). By doing this we can highlight why GTR is unnecessary and why Newtonian physics, despite the problems with Newton’s theories, accurately interprets the reality of the Jupiter-Sun relationship.
GTR ‘maths’
We can summarise the maths used by Einstein.
Gμν is the Einstein tensor, which describes the curvature of spacetime
Λ is the cosmological constant
gμν is the metric tensor, which defines the geometry of spacetime
Tμν is the stress-energy tensor, which describes the distribution of mass and energy
G is the gravitational constant.
c is the speed of light
Let’s connect GTR back to Newton, mass calculcations and the equation used to derive the masses of planets.
· G is a fundamental constant in GTR, just as it is in Newtonian gravity.
· GTR uses the stress-energy tensor, which includes mass as a form of energy, to describe how mass and energy curve spacetime.
· GTR must, and does, reproduce the Newtonian equations in weak gravity situations, which requires the use of G.
If the equation used to derive the mass of Jupiter or the Sun is wrong, then GTR is wrong. But that is only the beginning.
Using GTR
In GTR, unlike with Newton, there is no absolute. Space is not an absolute but is fraudulently merged with time. Many posts on here discuss why this is both impossible and insipid. But we need to accept this incorrect starting point when working with GTR. Light speed is also variant, which again disproves GTR. But still we persist.
Applying Einstein’s tensor calculus to the Jupiter-Sun relationship and attraction.
Step 1. Choose a ‘Coordinate System’:
GTR would employ the spherical coordinates (r, θ, φ) to take advantage of the Sun's spherical symmetry.
Step 2: Define the Stress-Energy Tensor (Tµν):
We need to model the mass distribution of the Sun. Within GTR we can approximate the Sun as a spherically-symmetric, non-rotating mass, which simplifies Tµν.
Note that the GTR assumption that the Sun does not rotate is false2.
We would use the Einstein Field Equations (Gµν = 8πGTµν) which now become the core equations we need to solve.
Step 3: Solving the Einstein Field Equations:
Calculate the Einstein Tensor (Gµν) which involves
1. Calculating the Ricci tensor (Rµν) and the scalar curvature (R),
2. Which are derived from the metric tensor (gµν) (step below)
3. These calculations involve partial derivatives of the metric tensor and Christoffel symbols (below)
Note that the Ricci, scalar calculations are based on unproven assumptions, and the tautological claim that space and time are merged.3
Step 4: Apply The Metric Tensor (gµν) to Ricci, and the scalar curvature:
Note this tensor simply assumes the geometry of spacetime.
In GTR we now need to find the specific form of gµν that satisfies the Einstein field equations.
For the Sun's weak gravitational field, the Schwarzschild metric would be used, but it is only an approximation.
Note that the Schwarzschild metric is tautological, assumes a static spacetime, a vacuum, a singularity, and a non-rotating sphere.4
Step 5: Apply the Christoffel Symbols (Γµνλ):
These symbols represent the "connection coefficients" that describe how the basis vectors of the coordinate system change from point to point.
Note, these symbols assume a curved spacetime and are unproven in reality.5
Γµνλ =21 gλσ (∂µ gνσ +∂ν gµσ −∂σ gµν)
Step 6: Put steps 3-5 together
Ricci Tensor (Rµν):
Rµν =∂λ Γµνλ −∂ν Γµλλ +Γµνλ Γλσσ −Γµσλ Γνλσ
Scalar Curvature (R):
R=gµνRµν
Step 7: Solve the Differential Equations:
In essence the Einstein field equations are a set of coupled, nonlinear partial differential equations and resolving them involves some fairly advanced mathematical techniques. Applying the above mathematics to Jupiter's Orbit we will need to formulate:
7.1 The geodesic Equation: Take the metric tensor (gµν), and use the geodesic equation to calculate Jupiter's orbit.
This equation describes the path of an object moving freely in the assumed curved spacetime.6
7.2 Also using the geodesic equation, we need to predict the elliptical nature of Jupiter's orbit which slowly precesses (wobble in the orbit).7
Result: It takes a small book to go through all the details, but in the end, the calculation derives an answer of approximately 4.16 × 10²³ newtons. This is a huge number which is difficult to comprehend. It means that the Sun is ‘pulling’ on Jupiter with a gravitational attraction that is 424,000,000,000,000,000,000,000 kilograms in weight, if we were to convert the mass of newtons, to kg of weight. That is 424 billion trillion kgs. Astonishing. At least this is what the math says. Is it true? Who knows.
We should note that far simpler Newtonian maths derive the same answer. In the next post we will post how to resolve Jupiter’s relationship with the Sun, using Newtonian maths. Newton’s approach was validated through observation, mathematical application and common sense. It does not need to delve into torturing geometry to derive an answer.
The Problems
You can see for yourself the issues with this process.
1. The equations to derive the gravitational constant and the masses of planets might be incorrect.
2. Within GTR Spacetime is incorrectly assumed.
3. Different coordinates and vectors in space are assumed.
4. Sun is incorrectly assumed to be non-rotational.
5. Riemannian geometry is assumed to be valid.
6. Ricci’s tensor is based on Riemann’s maths.
7. Schwarzschild constants are tautological, assuming a static spacetime, a vacuum, a singularity, and a non-rotating sphere.
8. Christoffel symbols are unproven and incredibly complex to manipulate.
9. Christoffel calculations are derived from the metric tensor itself, which is dependent on Ricci tensor, Schwarzschild constants, themselves dependent upon Riemann’s maths.
Geodesic calcs are based on Christoffel symbols which may be invalid.
None of this would impress a farmer.
Bottom Line
When Herbert Dingle, the apostate and once foremost expert in the world on Relativity stated that few people in the world really comprehended the tensor calculus behind Relativity, he was spot on.
Besides the objections listed above, these field equations are nonlinear, making them tedious to resolve with more than one path to a solution. You could in theory, provide almost an infinite number of possible answers to any problem. This is because the tensors themselves are full of manipulations. You need to raise and lower indices and calculate covariant derivatives. Approximations, not exactitudes are used, and these can be changed or manipulated as well.
There is no ‘science’ here. It is Tesla’s claim that Relativity was ‘mathematical garb’ designed to titillate and impress. There are far easier and more scientific methods to describe physics and cosmology. Relativity is completely arcane and unnecessary.
All hail.
== Appendix
1 When astronomers try to measure a celestial body mass, there are using a measurement of gravitational influence based on Newtonian physics, not GTR. Newton's laws of gravitation provide the mathematical foundation for these measurements though there are assumptions made.
For example: to calculate the Sun's mass, ‘the science’ observes the orbits of the planets; to calculate Jupiter's mass, they observe the orbits of its moons; to calculate Earth's mass, they can observe the Moon's orbit, or the orbits of artificial satellites.
This means that any mass calculation is fairly arbitrary and based on a series of assumptions. We should not assume that they are accurate.
n.b.:
Weight is the force of gravity on the object and is a vector measuring weight and direction, calculated in Newtons. Example the Apollo actor-nauts maintain they took a ~500 lb fold up jeep to the moon or 2224 Newtons. On the moon this would weigh ~70 lbs or ~300 Newtons.
A mass is the actual measure of an object's inertia, which is its resistance to changes in its motion and is measured in kg. (Mass calculations)
2 We can observe the Sun's rotation by tracking the movement of sunspots and other surface features across its disk. There is also differential rotation. The Sun is a giant ball of plasma, and it exhibits differential rotation. This means that different parts of the Sun rotate at different speeds. The Sun rotates faster at its equator than at its poles (similar to the Earth).
3 Base assumption is accepting Riemann’s geometry which is unproven and tautological. Mathematicians Gregory Chaitin and John Littlewood criticised Riemann’s abstruse equations for a lack of physical proof.
Chaitin, "Meta Math!: The Quest for Omega" (2005); "Littlewood's Miscellany" (1953, edited by Béla Bollobás).
4Schwarzschild constant is completely arbitrary, unproven and assumes that ‘static’ spacetime is curved, there is a vacuum, objects don’t rotate, there is a singularity. Again, tautological, unproven, frankly ridiculous. Some valid criticisms here https://vixra.org/pdf/2202.0091v1.pdf
5Christoffel symbols assume tautologically, a curved spacetime and are derived from the metric tensor itself. They are best viewed as constants and fudges to make the equations work. https://arxiv.org/abs/1512.05760
6 The geodesic equation is very complex:
‘Geodesic’ = a straight line mapped to a curved surface or a curved space (notice the assumption)
xμ: These are the coordinates of the object in spacetime. The index μ runs from 0 to 3, representing the time coordinate and the three spatial coordinates.
τ: This is the proper time, which is the time measured by an observer moving along the geodesic.
Γα (βμ): Are the Christoffel symbols, which encode the curvature of spacetime. They are calculated from the metric tensor, which describes the geometry of spacetime.
dxα/dτ and dxβ/dτ: Object's velocity along the geodesic.
d2xμ/dτ2: Acceleration of the object along the geodesic.
Explanation: Acceleration of an object along a geodesic is determined by the Christoffel symbols and the object's velocity. The Christoffel symbols, in turn, depend on the metric tensor, which is determined by the distribution of mass and energy in spacetime! Tautological.
In simpler terms: The equation describes how objects "fall" along the "straightest possible paths" in a curved spacetime. It is the mathematical expression of how gravity influences the path of an object.
7 Precession refers to a change in the orientation of the rotational axis of a rotating body or its wobble, in the direction that it is pointing. An example is the Earth's Precession. The Earth's axis wobbles, meaning its orientation slowly changes, and is reflected in the equinoxes. https://www.merriam-webster.com/dictionary/precession






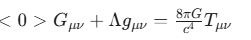




This all calls to mind an apologetic I once read about the Catholic Church’s treatment of Galileo. The historical fact is that Galileo was not convicted of heresy by the Church for teaching heliocentrism. He was punished for 1) Claiming scientific proof of heliocentrism where there was none, and 2) including a cartoon in his textbook portraying the pope as a clown. The same cast of characters who suppressed reasonable rebuttals of STR and GTR also used the Church’s alleged persecution of Galileo to hammer their detractors.
For brilliantly crafted words of wisdom deployed on the front lines of Substack, lock and load with the intellectual ammo Dr. FS3 so generously supplies from his armory.
There are no brainless frontal assaults here—only precision strikes and masterfully devised battle plans that hit the enemy where it hurts, earning his troops some well-deserved R&R in the officers’ mess.